INAO 2020 Question Paper Indian National Astronomy : olympiads.hbcse.tifr.res.in
Organisation : Homi Bhabha Centre for Science Education
Exam Name : INAO Indian National Astronomy Olympiad 2020
Document type : Question Paper
Website : https://olympiads.hbcse.tifr.res.in/
HBCSE INAO Exam
Homi Bhabha Centre for Science Education, INAO Indian National Astronomy Olympiad 2020 Question Paper.
Related / Similar Post : IISER Aptitude Test 2020 Sample Question Paper

INAO Question Paper
1. (10 marks) On the evening of an autumnal equinox day Siddhant noticed that Mars was exactly along the north-south meridian in his sky at the exact moment when the sun was setting. In other words, the Sun and Mars subtended an angle of exactly 90 as measured from the Earth. If the orbital radius of Mars is 1:52 au, What will be the approximate rise time of the mars on the next autumnal equinox day?
2. Manoj was determined to claim some world record. He got an idea from the fairy tale of Rapunzel that he will never cut his hair and he can claim world record for growing longest hair.
(a) (3 marks) Estimate maximum length of the hair that he can grow in his whole life, if he hasn’t cut his hair from his birth.
(b) (7 marks) What will be mass of these hair? (density of typical hair strand is 1:3 g=cm3)
If you make any simplifying assumptions, discuss qualitatively how answer would have been aected if those assumptions were not made.
3. (10 marks) A curious middle school student wants to actually measure perimeter of a circle of radius 2 cm. He has a scale and plenty of time at his disposal, but does not have a thread to measure lengths along arcs. Hence, he comes up with the following strategy:
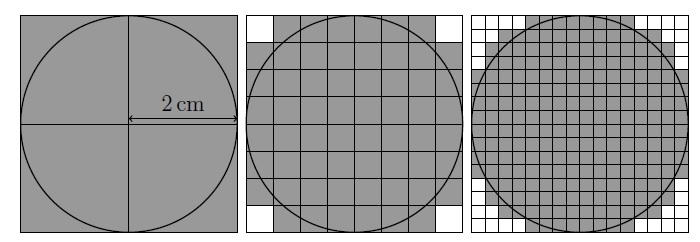
1. He makes a circumscribing square of the circle.
2. He divides the square into 4 equal smaller squares (left panel).
3. He measures the outer boundary (perimeter) of a shape formed by all the squares that overlap (fully or partially) with the circle (shape is highlighted in gray in the gure). He calls this estimate as P1.
4. He then makes a ner grid by dividing each smaller square into 4×4 grid. He again repeats step 3 to estimate the perimeter and calls it P2 (middle panel).
5. He keeps refining the grid again and again n times and nds nal estimate Pn.
Estimate Pn.
Hint: Eliminate white squares one by one, starting from corners, to arrive at the perimeter of gray shape.
4. Let us consider three stars A, B and C. It was observed that
** As seen from star B, star A is barely visible to the naked eye,
** As seen from star C, star B is barely visible to the naked eye,
** As seen from star A, star C is barely visible to the naked eye,
Let us denote the distance between star A and star B as d1, and distance between star B and C as d2 and star C and A as d3.
Absolute magnitude of star A, i.e. MA = 2:00 mag and that of star B is MB = 3:00 mag.
(a) (4 marks) Find the distances d1 and d2.
(b) (5 marks) Find the interval (in magnitudes) in which the absolute magnitude MC has to belong so that the above described conguration is allowed.
(c) (3 marks) If MC = 4:00 mag, nd the largest angle in this stellar triangle.
(d) (6 marks) Show that if we change the values of the three absolute magnitudes so that their dierences remain the same, the angles in the triangle will not change.
5) Pulsars are a type of fast rotating, high density stars, which are known for their regular pulses of radiation. They are also sometimes called as the `light houses of the universe’. In this problem, we assume the pulsars to be spheres of uniform density, which are gravitationally bound.
(a) (4 marks) Rotation period of a pulsar was measured to be P = 1:500 ms. What limit does this put on its density?
(b) (2 marks) If mass of this pulsar is 1:5M, what limit can we place on its radius? A pulsar is formed from a massive progenitor star which typically has a magnetic eld of 0:1T and average density of 10??4 g cm??3. Such a star loses about 90% of its mass towards the end of its life. The remnant mass forms a pulsar of the kind described above.
(c) (2 marks) Along the lines of part (a), what limit does this put on the rotation period of the progenitor star?
(d) (4 marks) Assuming that the magnetic flux is conserved during the formation of a pulsar, find the typical magnetic eld at the surface of the pulsar?
6) The picture below was taken on 24th December 2019, from some place in India, showing the crescent of the Moon near the horizon (the horizontal dashed line marks the horizon of the place). Field of View (FOV) of the image is 60.
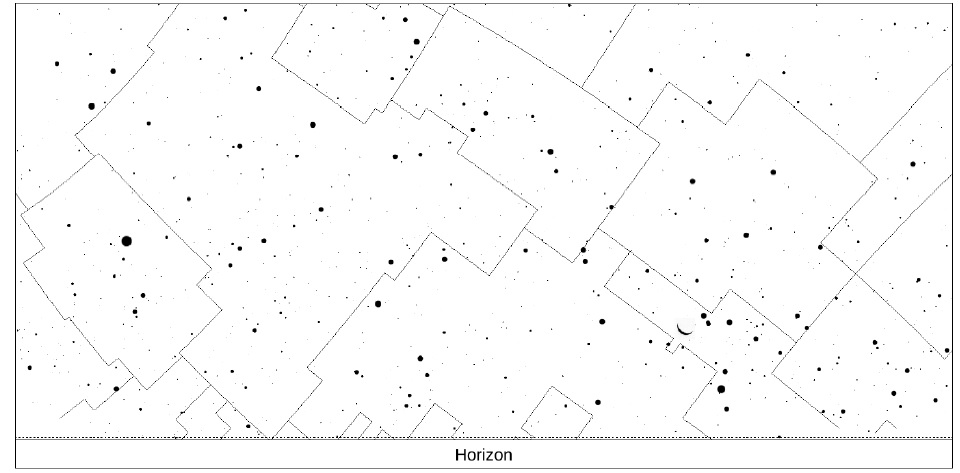
Note: The images printed are colour-inverted, i.e. the bright parts of the image appear black and dark parts appear white. Thus, the black dots are stars and planet and the dark cresent is actually bright crescent of the moon
(a) (5 marks) At which of the following times this picture may have been taken? Give justification for your answer. 18:00 hrs, 22:00 hrs, 01:00 hrs, 05:00 hrs
(b) (5 marks) Write the names of the constellations present in the image of the sky.
(c) (1 mark) The map also includes a planet. Mark the planet on the map with a circle and label as `P’.
(d) (5 marks) A zoomed-in image of the lunar crescent is given in the answersheet. On this image mark the approximate directions to the cardinal points. [East-West-North-South] Note: You may assume the box in the answersheet has a linear angular scale along the horizon.
(e) (4 marks) Find approximate latitude of the place.
Downloads
INAO 2020 Question Paper : https://www.pdfquestion.in/uploads/pdf2020/36963-IA.pdf